Haversine - the arc distance between points on a sphere.

Distance

As humans, we have multiple ways of intuitively understanding distance. Temporal, emotional and spacial distance are just some of the examples that come to mind. For the moment, we will focus on the latter.
Spatial distance is indeed pretty intuitive for most people. We can perfectly well guesstimate our position in this world. Currently, I am in Enschede. If you are reading this in Hengelo, there is approximalty a ten minute drive between us -- about five kilometers. I am looking at the next desk over; 3 meters. My cup of coffee: 20 centimeters. For my imperially challenged friends, that is a little under 8 inches. En fait, here is a little converter for your convenience:

When we think about our immediate surroundings, we like to estimate distances in a straight line. We can get away with this because - as far as our immediate surroundings are concerned - the Earth is almost flat. If you have ever looked at a globe, however, you will have noticed that the Earth's surface curves. And quite significantly too; it is pretty much a big round ball.
Measurements have shown that the Earth is not exactly a sphere, but an irregularly shaped ellipsoid. The most common way to deal with this complication is to ignore it. It only introduces a small error in our calculations, and it is not worth the effort for most applications.

So now, when we talk about distances over, say, a few kilometers (…or miles), we must take this curvature into account. We want to determine the distance between two points on the surface of Earth as the crow flies.

Let's dive into one of the most popular methods to calculate this, and try to understand it intuitively.

The haversine formula

The haversine formula was discovered in the early 19th century. It revolves around the haversine function. From Wikipedia, we find it is defined as $$\mathrm{hav}\left(\theta \right)={\sin }^2\left(\frac{\theta }{2}\right)$$
Using this function, the haversine formula is $$\mathrm{hav}\left(\theta \right)=\mathrm{hav}({\phi }_2-{\phi }_1)+\cos \left({\phi }_1\right)\cos \left({\phi }_2\right)\mathrm{hav}({\lambda }_2-{\lambda }_1)$$
with φ and λ the latitude and the longitude of the two points respectively. To solve for the distance d between the two points, we must take the inverse haversine: $$d=r\mathrm{archav}\left(h\right)$$
where r is the radius of the Earth.

If you are looking for the definition of the formula, there you have it. You can copy/paste this into your paper or code and it will not fail you. But if you are like me - curious why this works - read on!

Spherical coordinates

The haversine builds upon the idea of spherical coordinates. The coordinate systems most of us are familiar with are Carthesian. They consist of orthogonal axes in either two or three dimensions. Examples of this are the position of the mouse cursor on your computer screen. The coordinate system is Carthesian, the unit of measure is pixels. The position of the cursor is then a tuple of the horizontal pixel and the vertical pixel. In three dimensions, we have another axis for depth. If you have ever played a video game, you could imagine how the position of your character changes in the game's coordinate system as it walks, runs, jumps around.

A less intuitive coordinate system (and definitely less prominently present in daily life) are spherical coordinates. Even though we may not have many relatable examples of this to draw from, I believe most of us are somewhat familiar with how we describe positions on Earth. The generally accepted way of doing this is called the Geographic Coordinate System (GCS). This is also what your GPS uses. A position is a tuple of latitude and longitude. What sets the GCS apart from - for example - screen coordinates, is that its units are degrees, and that the surface it is projected on is not flat, but spherical. The origin of the GCS coordinate system is the center of the earth, but the origin of its projection on the globe is Null Island.
Latitude lines encircle the globe with horizontal rings. Longitude lines all pass through the same point on the north- and south pole. Zero degrees latitude lies on the equator, and zero degrees longitude passes straight through Greenwich, UK.

Since the haversine deals with positions on the surface of the Earth, it is also described in a spherical coordinate system. Of course there are ways of projecting Carthesian coordinate systems onto a sphere and vice-versa, but they are distinctly different representations.

Even though the GCS coordinate system is very widely used, it is not a very standard way of dealing with angles and positions in mathematics. The mathematical definition of spherical coordinates requires a fixed reference coordinate system. A point is then described by a radial distance from the origin of that system, a polar angle from a determined fixed axis, and an azimuthal angle, which is the point's orthogonal projection on a reference plane that passes through the origin and is orthogonal to the fixed (polar) axis, as measured from another fixed axis on that plane. Note that the intersection between this plane and the Earth is the equator. Wikipedia is again very helpful by providing a plot that illustrates this. The radial distance is r, the polar angle is theta, the azimuth is phi.

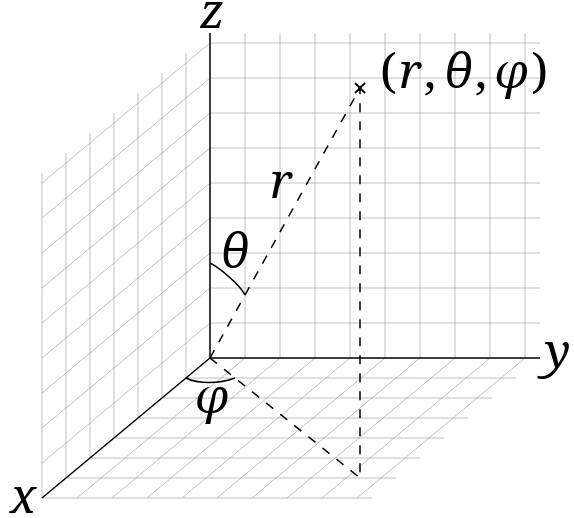
GCS coordinates have a mapping to such spherical coordinates. Firstly, since we are talking specifically about Earth, the radial distance is a constant R, which is approximately 6,371 kilometers. We can then find a mapping from a latitude to theta, taking the north pole as our polar reference axis. Similarly, we can map to phi by defining Greenwich to lie exactly on the reference axis for our longitude. By doing so, we bring the GCS coordinates into the more standard coordinate system the haversine makes use of.

Carthesian vectors and spherical coordinates

I have already mentioned there are ways to map points in spherical coordinates to Carthesian coordinates and the other way around. This is true because they represent the same information; only in different ways. We can do these transformations whenever we like, and in particular to make the math easier.

Let's remind ourselves of the objective here. We want to find the "as-the-crow-flies" distance between two points of Earth. This is the same as finding the arc distance between two points on the surface of some sphere. What is given is two points in GCS coordinates. What we want to find is just a single scalar. We realise we can change the given GCS coordinates into more standard spehrical coordinates. And now that we have those, how do we proceed to find the arc distance?

We can turn to our intuitive friend Descartes for help; let's map the points from spherical coordinates to Carthesian coordinates. In fact, let's invite Euclid to the party and describe those Carthesian coordinates using vectors! We'll call one vector v, and the other w. We will reuse the greek letters theta and phi to refer to the polar angles of vectors v and w respectively. We define the azimuth angle beta to be the angle between the orthogonal projections of v and w onto the reference plane (capturing the difference in longitude). We obtain: $$\overrightarrow{v}=R\left(\begin{array}{c}\cos \theta \\ 0\\ \sin \theta \end{array}\right)$$ $$\overrightarrow{w}=R\left(\begin{array}{c}\cos \phi \cos \beta \\ \cos \phi \sin \beta \\ \sin \phi \end{array}\right)$$ We should note the following: 1) the distance between the two points on the surface of the sphere is independent of our choice of reference coordinate system, and 2) the maths become a lot easier by pretending like point v lies on zero degrees longitude.

Derivation

We will be using some high school-level math to derive this haversine for ourselves. Having obtained Carthesian vectors for both ours points, we realize it is sufficient to find the angle α between vectors v and w. This in combination with the constant R (the radius of the Earth) allows us to find the arc distance d between the two points.

There is a convenient way to obtain alpha, and that is based on the dot product of v and w. The definition of the dot product is: $$\overrightarrow{v}.\overrightarrow{w}=||\overrightarrow{v}||||\overrightarrow{w}||\cos \alpha$$ This yields: $$\cos \alpha =\frac{\overrightarrow{v}.\overrightarrow{w}}{||\overrightarrow{v}||||\overrightarrow{w}||}$$ and knowing that $$||\overrightarrow{v}||=||\overrightarrow{w}||=R$$ we get $$\cos \alpha =\frac{\overrightarrow{v}.\overrightarrow{w}}{R^2}$$

To get the fraction out, we will move $R^2$ to the left. To obtain alpha, we simply expand the dot product: $$R^2\cos \alpha =\cos \theta \cos \phi \cos \beta +\sin \theta \sin \phi$$ Taking the arccos of this should give us the angle alpha we're looking for. However, even though this works out algebraically, the limited precision of floating-point numbers in computer proccessors make it so that the arccos becomes very imprecise for values near zero. Since we are talking about a sphere the size of a planet (literally), as small imprecision in alpha may result in a large error when calculating the arc distance. Instead, we can use the arcsin function, which performs much better under these conditions. We'll be using several trigonometric identities to find the form we are after. Starting from the expanded dot product: $$R^2\cos \alpha =\cos \theta \cos \phi \cos \beta +\sin \theta \sin \phi$$ $$=\cos \theta \cos \phi (1-2{\sin }^2(\frac{\beta }{2}\left)\right)+\sin \theta \sin \phi$$ $$=\cos \theta \cos \phi -2{\sin }^2\left(\frac{\beta }{2}\right)\cos \theta \cos \phi +\sin \theta \sin \phi$$ $$=\cos (\theta -\phi )-2{\sin }^2\left(\frac{\beta }{2}\right)\cos \theta \cos \phi$$ $$=1-2{\sin }^2\left(\frac{\theta -\phi }{2}\right)-2{\sin }^2\left(\frac{\beta }{2}\right)\cos \theta \cos \phi$$ Now using that $$\frac{1-\cos (\theta -\phi )}{2}={\sin }^2\left(\frac{\theta -\phi }{2}\right)$$ we get $${\sin }^2\alpha =\frac{1-(1-2{\sin }^2(\frac{\theta -\phi }{2}\left)\right)-2{\sin }^2\left(\frac{\beta }{2}\right)\cos \theta \cos \phi }{2}$$ $$={\sin }^2\left(\frac{\theta -\phi }{2}\right)-\cos \theta \cos \phi {\sin }^2\left(\frac{\beta }{2}\right)$$ And finally: $$\alpha =\arcsin \sqrt{{\sin }^2\left(\frac{\theta -\phi }{2}\right)-\cos \theta \cos \phi {\sin }^2\left(\frac{\beta }{2}\right)}$$ Do note that this arcsin form is actually less accurate than the arccos form when the two points are very far away from each other. It seems that there is no silver bullet. For my particular application (continental logistics), the arcsin is a better fit.

To conclude...

We have looked at one of the most common methods of dealing with finding the distance across a spherical surface between two arbitrary points. The real-world applications of this are numerous, and it's nice to have learned more about the technique. I don't know if it has gotten any more intuitive from my explanation and derivation of it, but just writing it down has helped me immensely. Thanks for bearing with me.

Note: it looks like Wikipedia has gotten wind of my critisism; they have since updated their article. It's pretty good, you could've just read that instead.